MCMC sampling examples

Goal: Explore a joint teaching approach, where I teach students both how to code in R in order to solve a real interesting problem rather than super basic stuff.

• consider starting with estimating PI with rejection sampling approach

library(brms)

We want to sample from a distribution. We know it’s density function, but imagine we don’t have a function that generates random samples. There are many ways to do it, but here we’ll illustrate MCMC methods:

• metropolis (in progress)
• rejection sampling
• hamiltonian
• adaptive…

We’ll also take an opportunity to see how we might optimize the code.

Metropolis Monte Carlo

Version 1: Naive implementation

Purposefully bad slow code, but works. We have our standard components:

• a pdf to evaluate (f)
• an initial value
• a proposal distribution
• a fixed number of mcmc samples to target

We iterate with a while loop and append accepted samples to a vector x until the length of the vector matches the number of samples.

• illustrate function factories and what they do for us here (perhaps a previous example without them, hard-coding the functions)

mcmc_metropolis1 <- function(f, init, proposal_dist, samples) {
  x <- init
  while (length(x) < samples) {
    x_ <- proposal_dist(1, x[length(x)])
    f1 <- f(x[length(x)])
    f2 <- f(x_)
    if (runif(1) <= f2/f1) {
      x <- c(x, x_) 
    } else {
      x <- c(x, x[length(x)])
    }
  }
  x
}

# TODO: check if can be done with distributional
dist_vonmises <- function(mu, kappa) {
  function(x) brms::dvon_mises(x, mu = mu, kappa = kappa)
}

dist_norm <- function(sd) {
  function(n, x) rnorm(n, mean = x, sd = sd)
}

out <- mcmc_metropolis1(
  f = dist_vonmises(0, 10), 
  init = 0.5, 
  proposal_dist = dist_norm(sd = 0.25), 
  samples = 2000
)

• add multiple traces in a subsequent example

here is our mcmc trace:

plot(out, type = "l")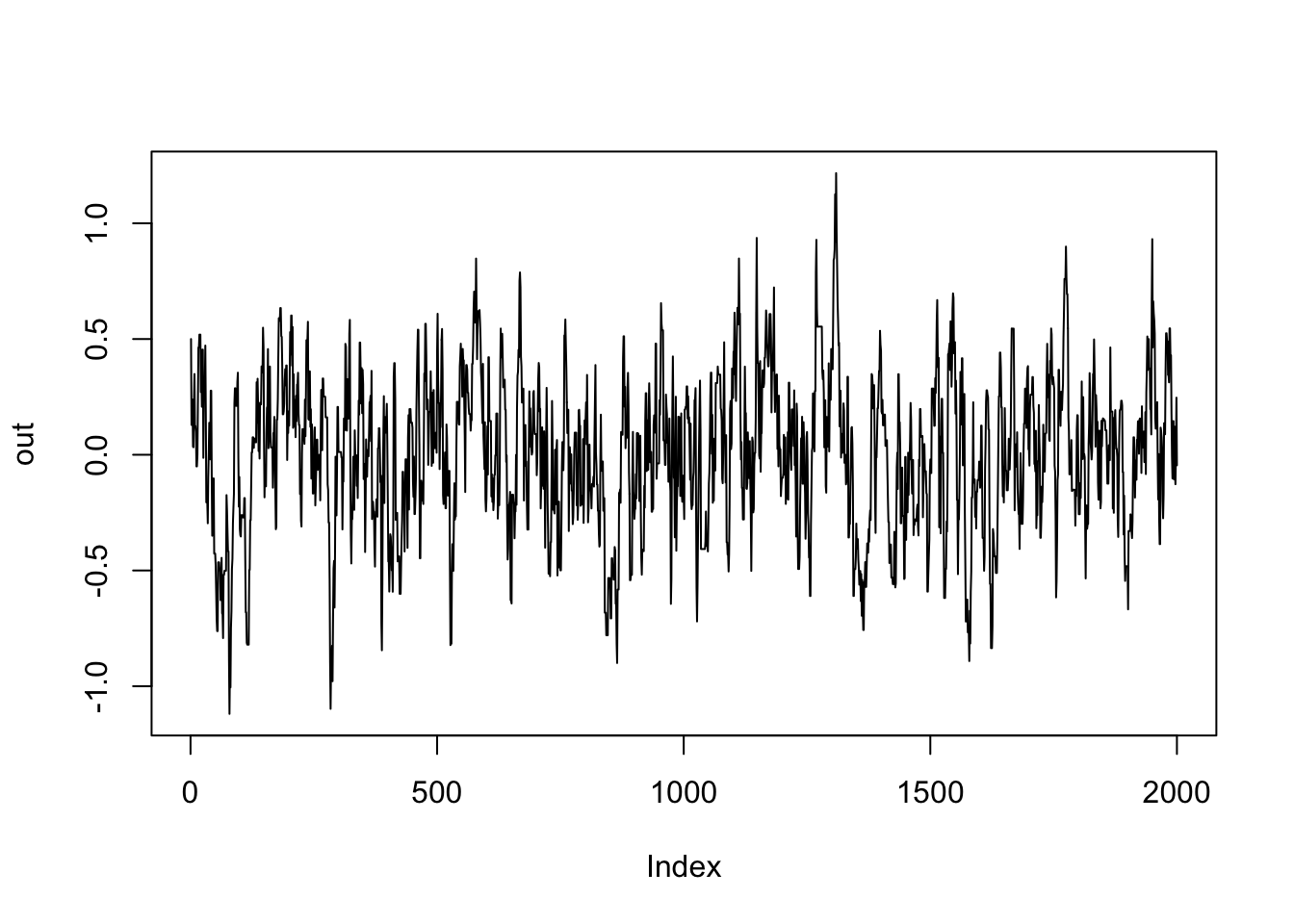

and the resulting distribution of samples, with the theoretical density on top:

plot(density(out))
curve(dist_vonmises(0, 10)(x), add = TRUE, col = "red")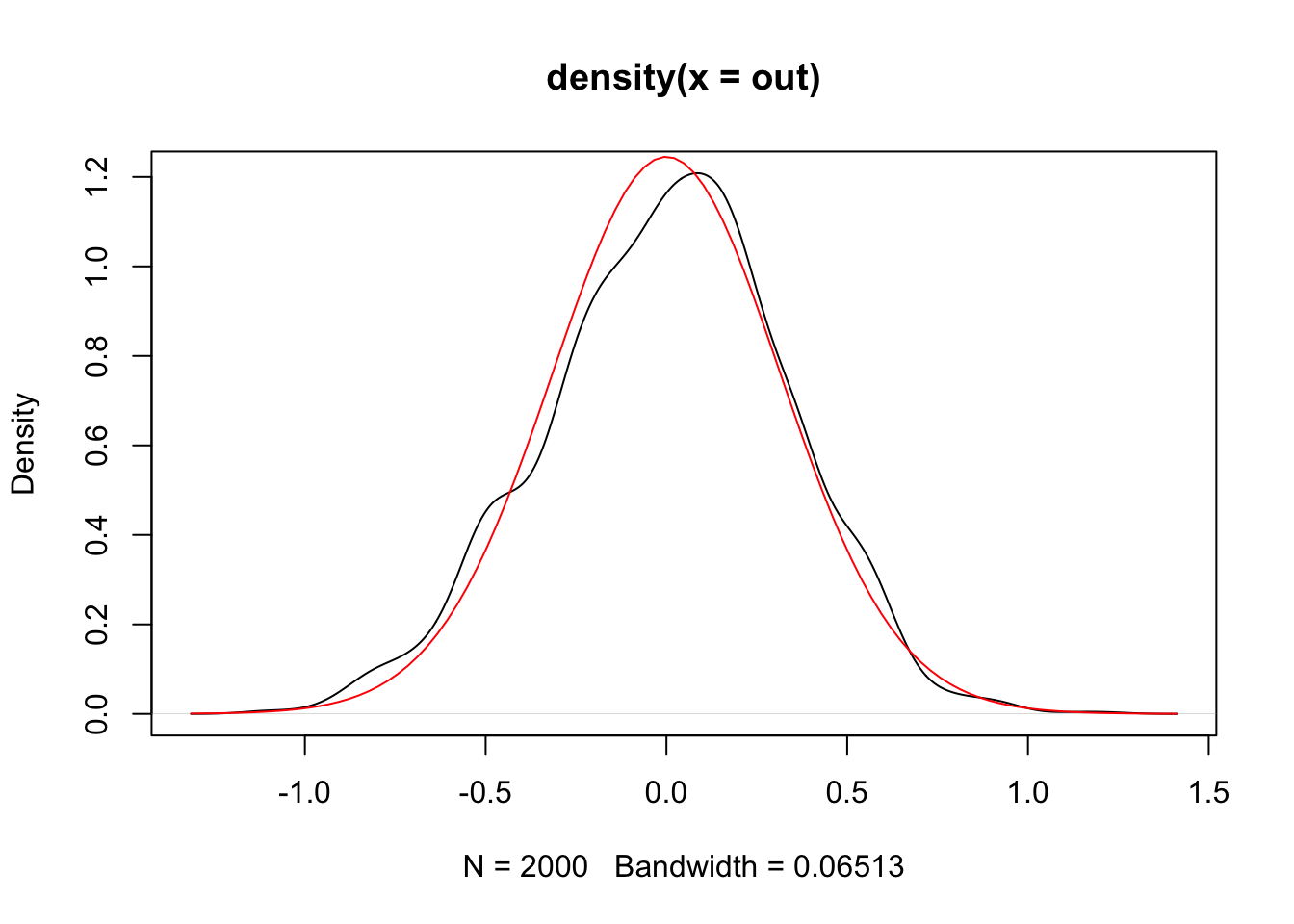

it runs fast because this is a really simple problem, but we can optimize our function a lot. Here are a few different ways to code the same algorithm:

mcmc_metropolis2 <- function(f, init, proposal_dist, samples) {
  out <- numeric(samples)
  f1 <- f(init)
  for (i in seq_len(samples)) {
    out[i] <- init
    x <- proposal_dist(1, init)
    f2 <- f(x)
    if (runif(1) <= f2/f1) {
      init <- x
      f1 <- f2
    } 
  }
  out
}

mcmc_metropolis3 <- function(f, init, proposal_dist, samples) {
  next_sample <- function(current, ...) {
    x_ <- proposal_dist(1, current)
    f1 <- f(current)
    f2 <- f(x_)
    if (runif(1) <= f2/f1) x_ else current
  }
  Reduce(next_sample, numeric(samples-1), init = init, accumulate = TRUE)  
}

mcmc_metropolis4 <- function(f, init, proposal_dist, samples) {
  next_sample <- function(current, ...) {
    x_ <- proposal_dist(1, current)
    f1 <- f(current)
    f2 <- f(x_)
    if (runif(1) <= f2/f1) x_ else current
  }

  out <- vector("list", samples)
  for (i in seq.int(samples)) {
    out[[i]] <- init
    init <- next_sample(init)
  }
  out
}

There are some speed differences among those, but they are all substantially better than the original.

bench::mark(
  mcmc_metropolis1(
    f = function(x) exp(10 * cos(x)),
    init = 0.5, 
    proposal_dist = dist_norm(sd = 0.25), 
    samples = 10000
  ),
  mcmc_metropolis2(
    f = function(x) exp(10 * cos(x)),
    init = 0.5, 
    proposal_dist = dist_norm(sd = 0.25), 
    samples = 10000
  ),
  mcmc_metropolis3(
    f = function(x) exp(10 * cos(x)),
    init = 0.5, 
    proposal_dist = dist_norm(sd = 0.25), 
    samples = 10000
  ),  
  mcmc_metropolis4(
    f = function(x) exp(10 * cos(x)),
    init = 0.5, 
    proposal_dist = dist_norm(sd = 0.25), 
    samples = 10000
  ),  
  check = FALSE 
)

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

# A tibble: 4 × 6
  expression                            min  median `itr/sec` mem_alloc `gc/sec`
  <bch:expr>                        <bch:t> <bch:t>     <dbl> <bch:byt>    <dbl>
1 mcmc_metropolis1(f = function(x)… 102.7ms 120.3ms      7.66     382MB    80.4 
2 mcmc_metropolis2(f = function(x)…  12.2ms  12.8ms     76.6      122KB     7.86
3 mcmc_metropolis3(f = function(x)…  17.9ms  18.7ms     51.1      349KB     9.83
4 mcmc_metropolis4(f = function(x)…  16.1ms  16.7ms     58.7      129KB     9.79

An alternative to the metropolis algorithm is rejection sampling:

rejection_sampling <- function(n, f, max_f, proposal_fun, ...) {
  stopifnot(is.numeric(n), length(n) == 1, n > 0)
  stopifnot(is.numeric(max_f), length(max_f) == 1 | length(max_f) == n, max_f > 0)

  inner <- function(n, f, max_f, proposal_fun, ..., acc = c()) {
    if (length(acc) > n) {
      return(acc[seq_len(n)])
    }
    x <- proposal_fun(n)
    y <- stats::runif(n) * max_f
    accept <- y < f(x, ...)
    inner(n, f, max_f, proposal_fun, ..., acc = c(acc, x[accept]))
  }

  inner(n, f, max_f, proposal_fun, ...)
}